Co tak naprawdę oznacza to podstawowe pojęcie kompresji bezstratnej?
Po co mi to wiedzieć?
Algorytm Huffman Coding jest blokiem konstrukcyjnym, z którego buduje się wiele algorytmów kompresji, takich jak na przykład DEFLATE - który jest używany przez format obrazu PNG oraz plik GZIP.
Załóżmy, że chcemy skompresować ciąg znaków (kodowanie Huffmana może być używane z dowolnymi danymi, ale łańcuchy znaków stanowią dobre przykłady). Nieuchronnie niektóre znaki będą pojawiać się częściej niż inne w skompresowanym tekście. Huffman Coding wykorzystuje ten fakt i koduje tekst tak, aby najczęściej używane znaki zajmowały mniej miejsca niż te rzadziej spotykane.
Zobaczmy to na przykładzie
Użyjmy kodowania Huffmana, aby skompresować zwrot do or do not. Słowo to ma długość 12 znaków. Ma też w sobie kilka zduplikowanych znaków, więc powinno się nam całkiem ładnie skompresować.
Dla celów argumentacji przyjmiemy, że przechowywanie każdego znaku zajmuje 8 bitów (kodowanie znaków to zupełnie inny temat). To zdanie kosztowałoby nas więc 96 bitów, ale możemy to zrobić znacznie lepiej z kodowaniem Huffmana.
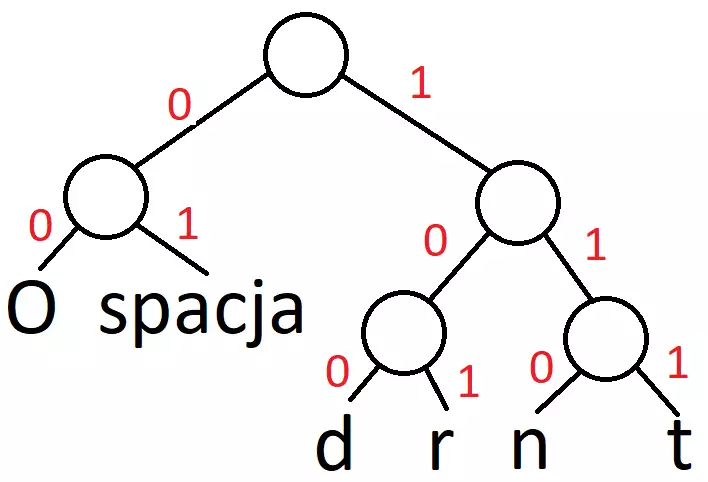
Zaczynamy od zbudowania struktury drzewa. Najbardziej powszechne znaki w naszych danych będą znajdować się bliżej korzenia drzewa, podczas gdy węzły najbardziej oddalone od korzenia reprezentują mniej powszechne znaki. Drzewo Huffmanna dla naszego zwrotu miałeś już okazję zobaczyć – jest to zdjęcie tytułowe tego artykułu.
Szukamy najpopularniejszych znaków
Najpopularniejszymi znakami w naszym ciągu są „o” (4 wystąpienia) i spacje (3 wystąpienia). Zauważ, że ścieżka do tych znaków znajduje się tylko dwa kroki od rdzenia, w porównaniu do trzech dla najmniej powszechnego znaku („t”). Teraz, zamiast przechowywać sam znak, możemy zamiast tego przechowywać ścieżkę do znaku.
Zaczynamy od węzła głównego i kierujemy się w dół drzewa w kierunku znaku, który chcemy zakodować. Będziemy przechowywać 0, jeśli pójdziemy ścieżką po lewej stronie, i 1, jeśli skręcimy w prawo.
Oto jak zakodowalibyśmy pierwszy znak, „d”, używając tego drzewa: 1 0 0. To są tylko 3 bity zamiast 8! Cały zakodowany ciąg znaków wyglądałby tak:
10000010010101100000111000111Tak – 29 bitów zamiast 96. I to wszystko w kompresji bezstratnej!
Dekodujemy, przesyłamy
Aby zdekodować nasz tekst, po prostu podążamy za każdym od samej góry w dół drzewa. Naszymi drogowskazami są „0” (mamy podążać lewą gałęzią) lub 1 (idziemy prawą gałęzią), aż dotrzemy do znaku. Zapisujemy ten znak a następnie zaczynamy ponownie od góry.
Ale zaraz… kiedy wyślemy zakodowany tekst do kogoś innego, czy on czasem też nie potrzebuje drzewa aby odkodować nasz przekaz? Oczywiście, że tak. Druga strona potrzebuje tego samego drzewa Huffmana, aby poprawnie zdekodować tekst. Najprostszym, ale najmniej wydajnym sposobem jest po prostu wysłanie drzewa wraz ze skompresowanym tekstem.
Moglibyśmy również najpierw uzgodnić drzewo tak aby zarówno nadawca jak i odbiorca używał tego samego drzewa podczas kodowania lub dekodowania dowolnego ciągu. Działa to dobrze, gdy możemy przewidzieć rozmieszczenie znaków z wyprzedzeniem i możemy zbudować stosunkowo wydajne drzewo bez sprawdzania, co najpierw kodujemy.
Sprawdź oferty pracy na TeamQuest
Inną opcją jest wysłanie wystarczającej ilości informacji, aby druga strona mogła zbudować to samo drzewo co my (tak działa GZIP). Moglibyśmy na przykład wysłać całkowitą liczbę przypadków wystąpienia każdego znaku. Musimy być jednak ostrożni; istnieje więcej niż jedno drzewo Huffmana dla tego samego bloku tekstu, więc musimy upewnić się, że oboje konstruujemy drzewo dokładnie w ten sam sposób. Nie wierzysz? Otwórz np. ten generator drzewa Huffmana i wygerenuj drzewko dla „do or do not” – będzie inne niż nasze.